Data structures
Table of Contents
Arrays
An array is a list of elements all of the same data type (e.g. all integers or all strings, not a mixture).
Each item in the list has an index, which describes its location in the list. The indexes begin at 0.
For example, this shopping list is an array containing strings:
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Value | "Apples" | "Bread" | "Milk" | "Corn" | "Butter" |
Finding items by index
You can get items in an array by looking up their index.
For example, you can find the first item with the expression arrayName[0] (remember, the first item is index 0). arrayName[4] would return "Butter" in the example above.
Arrays in Java
Arrays in Java are static
Arrays in java are static. This means they are of fixed length. The length is specified when you initialise the array.
This does not mean the array needs to be 'full' (i.e. have an item stored at each index). However, an array can never exceed its initial length and any attempt to add items beyond this maximum will cause an error.
Java code example
int[] grade = new int[3]; // Create an empty array of size 3 to store integers.
// OR you can initialise an array with values.
int[] grade = {87, 93, 35}; //Create an array populated with 3 integer values
System.out.println( grade[0] ); // Prints 87, the item at index 0 in the list.
System.out.println( grade.length ); // Prints 3. There are 3 items in the list
2D Arrays (Grid-like)
A 2D array is an array made up of arrays. It can be visualised as a grid or table (e.g. Excel spreadsheet).
Examples
Digital images are 2D arrays. Each pixel is a cell in the grid.
In Java
int rows = 3;
int columns = 4;
double[][] scores = new double[rows][columns]; // Defines a 3x4 table or grid
You can access an item in a 2D array using the row and column index, arrayName[rowNum][colNum] e.g. arrayName[0][0] is the first item in the first array (in the top left of the grid).
For the java code above, we could access the value in each cell as follows:
| Indexes | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | scores[0][0] | scores[0][1] | scores[0][2] | scores[0][3] |
| 1 | scores[1][0] | scores[1][1] | scores[1][2] | scores[1][3] |
| 2 | scores[2][0] | scores[2][1] | scores[2][2] | scores[1][3] |
Stacks
A stack is a data structure where data is added or removed at one end only. This end is called the top. Imagine a stack of trays in caffeteria. A stack is: Last in, first out (LIFO).

"Wikipedia stacks diagram#/media/File:Lifo_stack.png)" licensed under CC0
Stack operations in java
push(x)
Adds x to the top of the stack.
pop()
Remove one element from the top. This operation takes no parameter. It can only take the top item.
size()
Returns the number of elements in a stack.
empty()
Returns boolean, true if stack is empty.
peek()
Return top item without removing it from the stack.Imagine peeking at the first card in a deck of cards.
Stacks are dynamic
Stacks need not be of fixed size. Stacks can shrink and grows as items are added or removed. You can, however, choose to make a stack with a maximum size, but this can cause errors e.g. stack overflow - see below.
Stack Errors
Stack overflow
push(x) to a full (fixed size) stack will cause an error.
Stack underflow
pop() (or peek()) to an empty stack.
Queues
Queues in computer are like human queues, items are added at one end and remove from the other. Queues are first in, first out (FIFO).
"Diagram representing data queues#/media/File:Data_Queue.svg)" by Vegpuff/Wikipedia is licensed under CC BY-SA 3.0
Queue operations
enqueue(x)
Add x to the back of the queue.
dequeue()
Remove the item at the front of the queue. This takes no parameter, it can only access the front item.
Graphs
Graphs are a non-linear, non-hierarchical data structure. A little like a web or a social network.
Graphs are made up of nodes and edges. Nodes represent "things" in the graph and edges represent the relationships between them.
Node - An element in the graph, e.g. a user on a social network, or a city on a map.
Edge - (Sometimes called an arc) A relationship between two elements, e.g. a friendship between two people on a social network, or a road between two cities.
Directed Edge - An edge which represents a one-way relationship, e.g. following someone on Twitter doesn't necessarily mean they follow you back.
Undirected Edge - An edge representing a two-way relationship, e.g. if two people are friends on facebook.
Cycle - This is where you can travel from a node back to itself without going along any edge more than once, e.g. traveling from London to York to Lancaster to Birmingham to London again.
Trees
Trees are a non-linear, hierarchical data structure. They have a similar appearance to a family tree or organizational diagram.
Trees begin at a single root node, which has child nodes -> child nodes are roots of their own subtrees. Example: the computer’s directory system is a tree. Additionally, trees are non-cyclical - they cannot contain any cycles (see graph definition above).
Advantages of Trees
Trees are so useful and frequently used, because they have some very serious advantages:
- Trees reflect structural relationships in the data
- Trees are used to represent hierarchies
- Trees provide an efficient insertion and searching
- Trees are very flexible data, allowing to move subtrees around with minimum effort
Common terminology:
Internal node - child with at least one child
External node - child without any children
Depth - number of ancestors a node has, i.e. how far down in the tree it is
Degree - number of children of a node
Height - maximum depth of any node
Traversal - A traversal is a process that visits all the nodes in the tree. Since a tree is a nonlinear data structure, there is no one way to traverse them.
Types of Traversal:
- Pre-order - visit the parent first and then left and right children
- In-order - visit the left child, then the parent and the right child
- Post-order - visit left child, then the right child and then the parent
As an example consider the following tree and its four traversals:

Pre-order: 8, 5, 9, 7, 1, 12, 2, 4, 11, 3
In-order: 5, 1, 7, 2, 12, 8, 4, 3, 11
Post-order: 9, 1, 2, 12, 7, 5, 3, 11, 4, 8
Level-order: 8, 5, 4, 9, 7, 11, 1, 12, 3, 2
Consider the flow of the different types of traversal on the following tree:

Binary Trees
A binary tree has a special condition that each node can have a maximum of two children. A binary tree has the benefits of both an ordered array and a linked list as search is as quick as in a sorted array and insertion or deletion operations are as fast as in linked list.
Example of a binary tree (from Wikipedia):
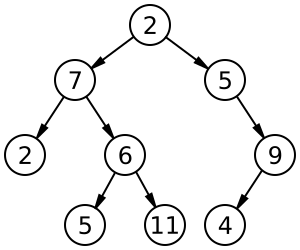
A complete binary tree is very special tree, it provides the best possible ratio between the number of nodes and the height.
Full versus Complete binary tree:

Binary Search Trees
A Binary Search Tree is a binary tree in which for every node, all the nodes in its left subtree have lower values than it, and all the nodes in its right subtree have higher values.
The basic idea behind this data structure is to have a storing repository that provides an efficient way of data sorting, searching and retrieving.
A Binary Search Tree (BST) is a binary tree where nodes are ordered in the following way:
- each node contains one key (also known as data)
- the keys in the left subtree are smaller then the key in its parent node
- the keys in the right subtree are greater the key in its parent node
- duplicate keys are not allowed
In the following tree, all nodes in the left subtree of 10 have keys < 10 while all nodes in the right subtree have keys > 10. Because both the left and right subtrees of a BST are also binary search trees, the above definition applies to all internal nodes:
